Extend a Function to a 2pi Continuous Function

Trigonometric functions

Here we will assume that you are familiar with angles and how they are measured, in particular with radians. If you are not sure, you can have a look at this note.

There are several ways to define trigonometric functions. We will briefly recall two of them, based on geometric ideas. Then we will look at properties of trigonometric functions, recall some trig identities, try to make some sense of their inverses and conclude with a brief note concerning secant and cosecant.

Geometric definitions

Unit cirlce. Let α be any angle. Consider a unit circle in the plain and the ray going from the origin at the angle α. Let (x,y) be the coordinates of the intersection of the ray and the unit circle. We then define

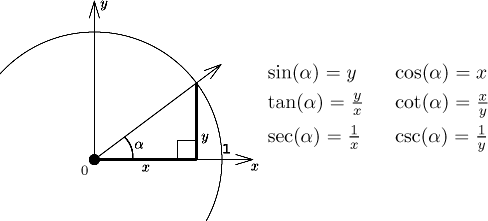
Of course, some definitions do not make sense if x = 0, resp. y = 0.

Clearly we then have

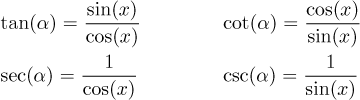
The functions sec(α) (secant) and csc(α) (cosecant) used to be very popular in the old days when people still had to calculate things by themselves, since they simplified calculations with trig functions. Today they are mostly forgotten and we include them here for the sake of completeness. We will return to them at the end of this section.

Note that when defined like this, all these functions are 2π-periodic, under closer inspection tangent and cotangent are π-periodic.

Right-angle triangle. Let α be an angle from the interval (0,π/2). Consider an arbitrary right-angle triangle with another angle equal to α. We then have the folowing definitions:

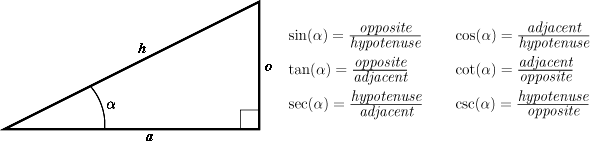
These functions are connected by the same formulas as above. How do we extend these definitions to any angle α? First we define sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.

For α from [π/2,π] we define sin(α) = sin(π −α) and cos(α) = −cos(π −α).

For α from [π,2π] we define sin(α) = −sin(α − π) and cos(α) = −cos(2π −α).

Thus we get sine and cosine on [0,2π], then we extend them to all angles by repeating this basic period. The other functions can be all defined using sine and cosine and the above formulas.

We conclude this part by recalling the values of sine and cosine for the popular angles:

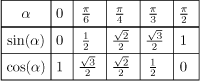
There is a simple way to remember these using the left hand.

Another practical remark, instead of writing [sin(x)] ⁿ we usually write sin ⁿ (x), similarly for other trig functions.

Properties of trigonometric functions

The sine. The domain:

D(sin) = ℝ.

The graph:

The function is continuous on its domain, 2π-periodic, bounded, and symmetric, namely odd, since we have sin(−x) = −sin(x). We also have

sin(x + π) = −sin(x), sin(x + π/2) = cos(x), sin(x − π/2) = −cos(x).

From the periodicity we have

sin(x + 2kπ) = sin(x), sin(x + (2k + 1)π) = −sin(x).

Zero points of sine are points of the form kπ, where k is any integer; these are also points of inflection. Local extrema are at the points π/2 +kπ.

Concerning limits at endpoints of the domain, limits of sine at infinity and negative infinity do not exist.

The derivative:

[sin(x)]′ = cos(x).

---

The cosine. The domain:

D(cos) = ℝ.

The graph:

The function is continuous on its domain, 2π-periodic, bounded, and symmetric, namely even, since we have cos(−x) = cos(x). We also have

cos(x + π) = −cos(x), cos(x + π/2) = −sin(x), cos(x − π/2) = sin(x).

From the periodicity we have

cos(x + 2kπ) = cos(x), cos(x + (2k + 1)π) = −cos(x).

Zero points of cosine are points of the form π/2 +kπ, where k is any integer; these are also points of inflection. Local extrema are at the points kπ.

Concerning limits at endpoints of the domain, limits of cosine at infinity and negative infinity do not exist.

The derivative:

[cos(x)]′ = −sin(x).

---

The tangent. The domain:

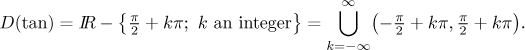
The graph:

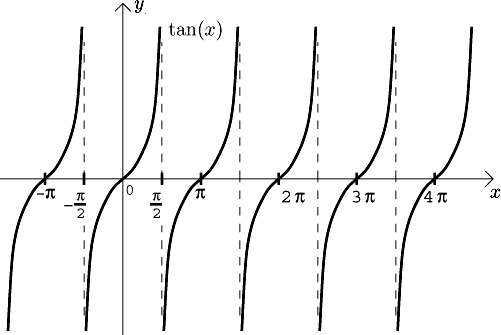
The function is continuous on its domain, π-periodic, not bounded, and symmetric, namely odd, since we have tan(−x) = −tan(x). We also have

tan(x + π) = tan(x), tan(π −x) = −tan(x).

Zero points of tangent are points of the form kπ, where k is any integer; these are also points of inflection. There are no local extrema.

Concerning limits at endpoints of the domain, limits of tangent at infinity and negative infinity do no make sense since the domain does not include any neighborhood of infinity or negative infinity. Limits at finite endpoints of the domain do not exist, but we have one-sided limits there:

The derivative:

[tan(x)]′ = 1/cos²(x).

---

The cotangent. The domain:

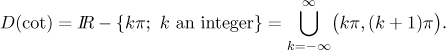
The graph:

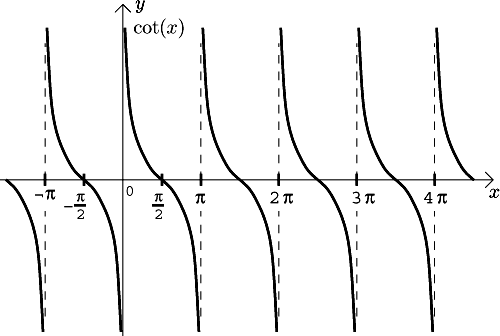
The function is continuous on its domain, π-periodic, not bounded, and symmetric, namely odd, since we have cot(−x) = −cot(x). We also have

cot(x + π) = cot(x), cot(π −x) = −cot(x).

Zero points of cotangent are points of the form π/2 +kπ, where k is any integer; these are also points of inflection. There are no local extrema.

Concerning limits at endpoints of the domain, limits of cotangent at infinity and negative infinity do no make sense since the domain does not include any neighborhood of infinity or negative infinity. Limits at finite endpoints of the domain do not exist, but we have one-sided limits there:

The derivative:

[cot(x)]′ = −1/sin²(x).

Trig identities

First some popular identities for sine and cosine.

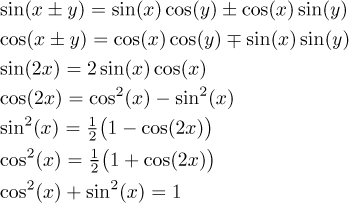
The following identities are less popular, but sometimes they are very useful.

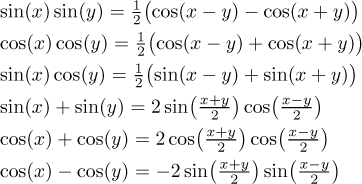
Sine and cosine can be also obtained (or even defined) using exponentials and complex numbers.

Finally, sometimes this trick is also useful.

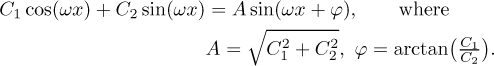
We have an obvious problem when C ₂ = 0. Then we can take φ = π/2 if C ₂ > 0  and φ = −π/2 if C ₂ < 0.

Now some popular identities for tangent and cotangent.

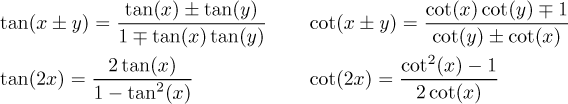
Since sine and cosine can be expressed using complex exponentials, the same is true for tangent and cotangent.

Finally, we will show some formulas that relate sine/cosine and tangent.

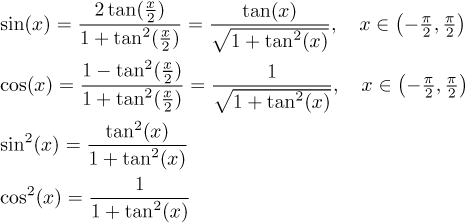
Inverse trigonometric functions

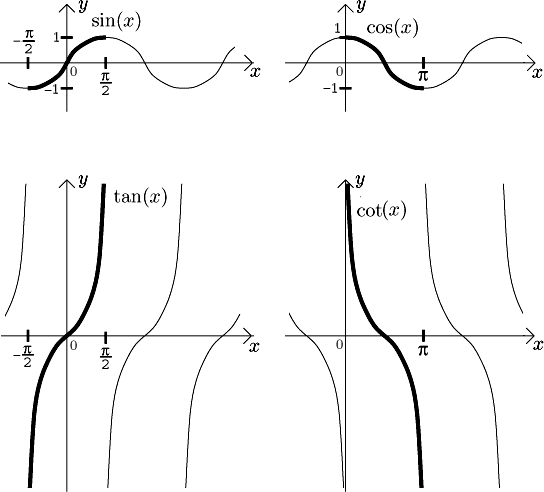
When we look at the graphs above, we see right away that none of the four basic trig functions is 1-1, so they do not have inverses. On the other hand, from practical point of view, some sort of inverse would be immensely useful, and indeed people were assigning angles to sides of triangles long before mathematicians came up with the notion of inverse. In order to do this properly we use the usual trick, we will restrict the trig functions to intervals on which they are already 1-1. We will choose intervals so that they are as large as possible (so that they cover the whole range) and also so that they give "reasonable" angles, meaning around 0. Indeed, it is more practical to learn that the angle in a triangle is 30 degrees then learning that it is 750 degrees (we should be actually using radians, but degrees are easier to imagine and type on the Web, so I made an exception here).

Inverse trigonometric functions. They are defined as follows. First we restrict the four trigonometric functions to intervals as indicated.

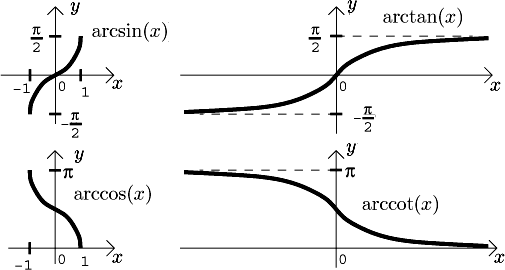
Then we consider inverses to these restrictions. They are called arc sine (denoted arcsin), arc cosine (denoted arccos), arc tangent (denoted arctan) and arc cotangent (denoted arccot). The graphs of these functions are here:

We now list the basic properties of these inverse trig functions. They are all continuous, monotone and bounded.

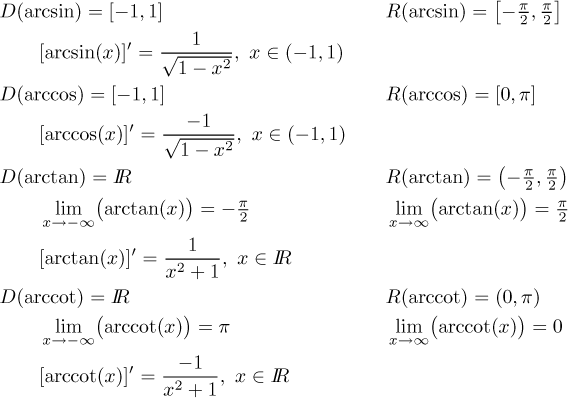
Note: Many authors (and most calculator makers) actually use a different notation, namely sin⁻¹(x), cos⁻¹(x) etc. This notation is extremely misleading and many students indeed see an admittedly strong similarity between sin⁻¹(x) and, say, sin²(x) for the square of sine; logically they then expect that sin⁻¹(x) is actually 1/sin(x). Of course, the inverse to sine and 1/sin(x) are entirely different functions. Although there is a reasonably good justification for this notation (see our exposition of inverse functions in Theory - Real functions), it is very unfortunate because of these misunderstandings. Since there is a perfectly acceptable alternative that is also widely known, namely those arc things, we will always use them here.

Remark: Let us return to the original question: We are given a number y and we want to find a number x satisfying, say, sin(x) =y. If this x is from the region to which we restricted sine a moment ago, then we have the solution x = arcsin(y). But what if for some reason we need x from a different part of the real line? Or taken from another point of view, if we restrict sine to a different reasonable interval, what would be the formula for the inverse function to such a restricted sine? (And of course also to cosine etc.) The following formulas are true:

• Let sin(x) =y.
  If 2kπ − π/2 ≤x ≤ 2kπ + π/2 for some integer k, then

  x = arcsin(y) + 2kπ.

  If (2k + 1)π − π/2 ≤x ≤ (2k + 1)π + π/2 for some integer k, then

  x = (2k + 1)π − arcsin(y).

• Let cos(x) =y.
  If 2kπ ≤x ≤ 2kπ + π for some integer k, then

  x = arccos(y) + 2kπ.

  If (2k + 1)π ≤x ≤ (2k + 1)π + π for some integer k, then

  x = (2k + 2)π − arccos(y).

• Let tan(x) =y.
  If kπ − π/2 <x <kπ + π/2 for some integer k, then

  x = arctan(y) +kπ.

• Let cotan(x) =y.
  If kπ <x <kπ + π for some integer k, then

  x = arccotan(y) +kπ.

There are very interesting formulas relating trig functions and their inverses. They are seldom used, but they are so cute we can't resist putting them here.

Secant and cosecant

We will just briefly review their properties. Graphs:

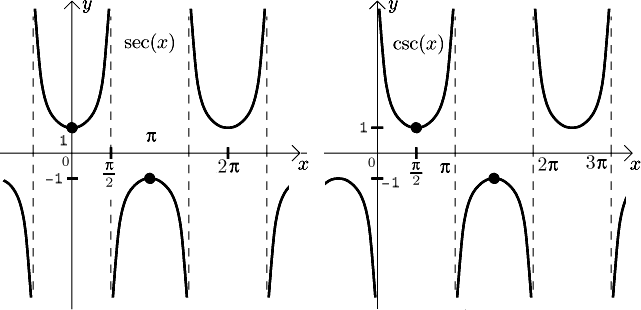
Derivatives:

---

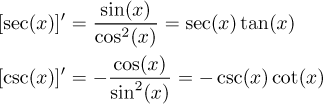
Hyperbolic functions
Back to Theory - Elementary functions

walkerupocand.blogspot.com

Source: https://math.fel.cvut.cz/mt/txtb/4/txe3ba4e.htm

Share this post